С 1995 года взамен качественных рассуждений о сытности тех или иных продуктов/блюд появилась возможность воспользоваться количественной мерой сытности – индексом сытости (ИС) продукта. Исследование проведено по аналогии с введенным в оборот в 1981 году гликемическим индексом (ГИ). ГИ родился в результате попытки создать наиболее благоприятное для людей с сахарным диабетом питание.
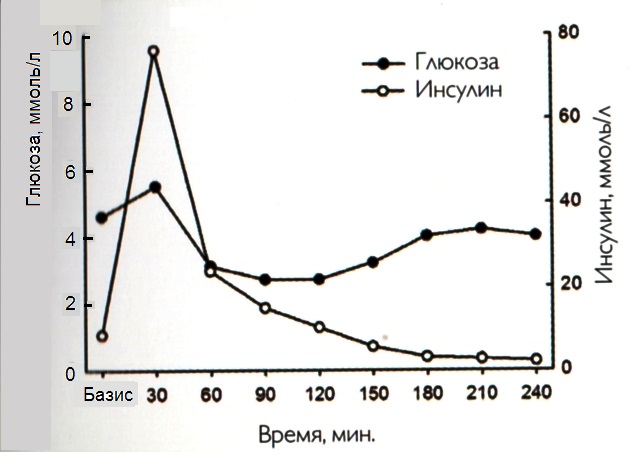
ГИ количественно оценивает способность продуктов влиять на содержание глюкозы в сравнении с одним из эталонных продуктов (глюкозой или белым хлебом), т.е. понятие ГИ расщеплено – существуют 2 разные шкалы, ГИ по хлебу в 1,38 раз больше ГИ по глюкозе, что приводит к недоразумениям, когда упоминается ГИ продукта без указания, по какой шкале он определен.
Поскольку ГИ не позволил прогнозировать, будет человек сыт или нет после употребления продукта с известным ГИ, степень насыщаемости после употребления продукта пытались привязать к гликемической нагрузке, инсулинемическому индексу, и все без определенного успеха.
На практике пользовались практическими правилами – больше белков, меньше сахара, добавление в рацион отрубей, и большое количество воды. Насчет жиров полной определенности не было – жиры то объявлялись сытными («жирного не поем – хожу голодный»), то бесполезными в плане насыщения.
Итак, переходим к проведенному в Университете Сиднея Сюзанной Холт с коллегами исследованию.
https://www.researchgate.net/publicatio ... mmon_foods
Участники эксперимента, которым предстояло экспериментально установить индекс сытости 37 продуктов – студенты университета в возрасте около 18-26 лет с нормальным индексом массы тела, при примерно равном количестве юношей и девушек, все некурящие, с нормальной толерантностью к глюкозе, не принимающие никаких медикаментов и не имеющие необычных пищевых пристрастий. Ни один из участников не придерживался специальной диеты, и все вели вполне обычный образ жизни.
Исследование частично обладало признаками «слепого» эксперимента – участники не имели никакого представления о его цели, их ввели в заблуждение, сказав, что назначение эксперимента – изучение метаболической реакции организма на разные продукты с целью отбора продуктов для питания диабетиков и спортсменов.
Индекс сытости (ИС) 37 тестировавшихся продуктов сравнивался с индексом сытости белого хлеба, для чего участникам в начале эксперимента предлагалось съесть порцию хлеба калорийностью 1000 кДж (или примерно 240 ккал). Это измерение использовалось в качестве эталонного для данного участника, в последующие дни предлагался исследуемый продукт, тоже в количестве, эквивалентном 240 ккал.
Продукт предлагался утром, натощак, после 10-часового пищевого воздержания. Накануне, чтобы исключить последействие, участникам предлагалось поужинать стандартно без каких-либо особенностей. Продукты в тех случаях, когда это было возможно, сервировались так, чтобы участники эксперимента как можно меньше знали, сколько продукта они съедают (чтобы исключить эффект внушения).
Продукт разрезался на части, тарелка накрывалась матовым колпаком с отверстием, через которое участник извлекал пищу по кусочкам, пока не съедалась вся предложенная порция. Некоторые продукты и блюда подавались традиционно (напитки и мороженое в чашках, каши и блюда под соусом на тарелках). На весь завтрак отводилось 10 минут, к завтраку подавались 220 мл воды, которую предлагалось непременно за завтраком выпить.
Каждые 15 минут с начала приема пищи на протяжении 2 часов участникам предлагалось оценить чувство сытости по 7-бальной шкале от -3 до +3, где -3 означало «очень голодный», -2 «голодный», -1 «полуголодный», 0 «без особых ощущений», 1 «полусытый», 2 «сытый», 3 «совершенно сытый». В тестировании каждого продукта по плану эксперимента предполагалось задействовать 12 участников, по факту участвовало от 11 до 13.
В течение 2 часов, когда участники оценивали степень сытости после употребления продукта, они не принимали пищу и не пили, им позволено было читать, вести беседу, слушать радио, но никоим образом не делиться своими индивидуальными впечатлениями о еде.
По выдаче через 2 часа с начала приема пищи последнего отчета участникам предлагался ланч по типу «шведского стола», всегда однообразный, с неограниченным количеством самых обычных продуктов – зерновых каш, хлеба и тостов с маргарином, джемом или австралийским пастообразным продуктом «веджемайт», бисквиты, фруктовые пироги, чай, кофе, апельсиновый сок, вода.
Во время ланча отмечался общий вес съеденных продуктов и их общая калорийность. После ланча участники были свободны до утра дня следующего эксперимента, где им предлагался уже другой тестируемый продукт.
По завершению эксперимента (тестирования всех 37 продуктов) производилась обработка полученных данных. Методика обработки и вычисления индекса сытости схожа с методикой вычисления ГИ, лишь вместо уровня глюкозы в крови использовалась субъективная оценка участниками степени своей сытости.
На графике зависимости степени сытости (от -3 до +3) от времени (от 0 до 120 минут, всего 8 отметок, без начальной отметки, соответствующей 0 минутам, которой условно приписывалась степень сытости 0 без опроса участников). Все точки графика соединялись отрезками прямых линий, и подсчитывалась площадь, ограниченная линией графика и горизонтальной линией, соответствующей степени сытости 0.
Все, что лежало ниже 0, из подсчета исключалось. Индивидуальный индекс сытости подсчитывался как умноженное на 100 отношение площади под кривой продукта к площади под кривой для белого хлеба (эталона). Далее вычислялся средний по группе из 11-13 тестировавших данный продукт участников индекс сытости, и точность оценки этого значения исходя из разброса отдельных значений.
Часть продуктов имела ИС ниже 100 (абсолютный минимум 47 для круассана), часть выше 100 (абсолютный максимум 323 для вареного картофеля). В точности равным 100 оказался ИС еще одного продукта (кроме эталонного белого хлеба) – мюсли с молоком. Стандартная ошибка индексов сытости изменялась в пределах от 19 до 62.
Авторы исследования определяли зависимость ИС от некоторых характеристик продукта, и пришли к выводу, что ИС прямо зависит от веса порции продукта (который, в свою очередь, обратно пропорционален калорийности 100 г продукта). Увеличение содержания жира приводило к снижению ИС, в то время как увеличение содержания белков, пищевых волокон и воды вело к увеличению ИС.
Относительно сахаров, крахмала и общего содержания углеводов исследователи пришли к выводу, что наблюдавшиеся зависимости признать значимыми не представлялось возможным.
Количество продуктов, употребленных за ланчем, при вычислении ИС не учитывалось, но служило контролем – большей сытности тестового продукта соответствовало в среднем меньшее количество (по весу и калорийности) употребленных за ланчем продуктов, и наоборот.

Значения индексов сытости продуктов от Сюзанны Холт (приведены выше) получили широкое распространение, но комментирование свелось в основном к качественным рекомендациям питаться продуктами:
• низкокалорийными (что повышает объем порции);
• маложирными (поскольку по данным авторов исследования жиры коррелируют отрицательно с индексом сытости);
• с высоким количеством белков и пищевых волокон (коррелируют положительно с индексом сытости);
• исключить сахара и минимизировать сложные углеводы (корреляция с индексом сытости близка к нулю).
Разумеется, при знакомстве с подобным материалом возникает желание подробнее разобраться с количественной зависимостью ИС от компонентного состава пищи, и первые же поиски навели на сайт http://nutritiondata.self.com/topics/fullness-factor, где приведена формула зависимости Fullness Factor™ (Коэффициент сытости). Вот она:
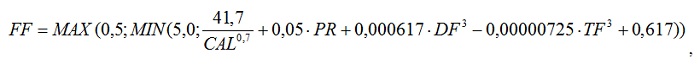
где CAL – калорийность продукта, ккал/100 г, PR – содержание белков, г/100 г, DF – содержание пищевых волокон, г/100 г, TF – содержание жиров, г/100 г.
По формуле подсчитаны коэффициенты сытости (КС) тех же самых 38 продуктов (тестированные С. Холт 37 продуктов и эталонный белый хлеб), и приведена диаграмма со сравнением экспериментальных и теоретических данных. Совпадение неплохое, но формула наводит на размышления. Во первых, автор отчего-то отказался от термина «индекс сытости» и ввел свой, вдобавок зарегистрировав его как товарную марку. Также он отказался от шкалы, где за 100 условно принят ИС эталона – белого хлеба, и ввел произвольную шкалу, единица измерения которой никак не определяется. Белый хлеб имеет по шкале FF™ коэффициент сытости 1,8, вдобавок устанавливается коэффициент пропорциональности между значениями по двум шкалам как 1:60, опять-таки без обоснования.
Так что не так с формулой, раз она хорошо предсказывает экспериментально полученные значения? Проблема в том, что получена она путем применения некоего математического формализма, позволяющего подогнать любую формулу под любые данные путем выбора коэффициентов. Но коэффициенты должны быть обоснованы исходя из каких-либо предпосылок, в данном случае физиологических. Смущает число подгоночных коэффициентов в формуле: это калорийность, процентный состав по белкам, жирам и волокнам, уже 4 коэффициента. Далее автор счел нужным отказаться от аддитивной модели, где вклад компонента в общую сытость прямо пропорционален его количеству.
Аддитивность нарушается тем, что 3 компонента из 4 дают вклад, пропорциональный не первой степени количества, а иной, подбираемой программой с целью наилучшей подгонки теоретических данных под экспериментальные. Показатели степени выбраны 0,7 при калорийности, 1 при белках (нет сомнения, что 1 тоже выдано программой, т.е. этот показатель степени тоже подгонялся), и 3 при жирах и волокнах, итого еще 4 подбираемых коэффициента. Возведение в куб вообще-то вызывает оторопь – неужто увеличение доли волокон в 5 раз дает увеличение вклада в сытость в 125 раз?
Следующий подгоночный коэффициент – свободный член 0,617, и совершенно уникальным является признак полной беспомощности – ограничительные коэффициенты 0,5 снизу и 5,0 сверху. Каковы бы ни были результаты вычислений (а третья степень по жирам и волокнам способна раздуть значение КС до неприемлемых отрицательных по чистым жирам и зашкаливающих до сотен единиц для чистой клетчатки). Отсюда искусственное ограничение значений КС в диапазоне от 0,5 до 5,0 с введением еще 2 подгоночных коэффициентов. Итого 11 коэффициентов для описания всего 38 значений. Не многовато ли?
Придется искать более вменяемую зависимость, интуитивно понятную и позволяющую предсказать ИС любого продукта с достаточной для практики точностью, с минимумом коэффициентов, и, самое главное – аддитивную. А потом попытаться объяснить на основе этой зависимости популярные диетологические рекомендации, направленные на уменьшение калорийности с одновременным повышением сытости диет.
Основой конструирования формулы ИС послужили данные С. Холт, где наряду с индексом сытости порции продукта в 240 ккал приводится состав порции, а именно: приведено количество белков, жиров, сахаров, крахмала, пищевых волокон и воды в порции (а не количество компонентов в 100 г, что общепринято), а также вес порции, который зависит от калорийности продукта и его состава.
Автор указывает, что состав и калорийность продуктов соответствуют данным производителя. Обширные данные обычно содержат ошибки, от типографских опечаток до принципиальных. Нами проверено предположение, что калорийность можно рассчитывать исходя из энергетической ценности белков и углеводов 4 ккал/г, жиров 9 ккал/г, пищевых волокон 0 ккал/г (фактическая энергетическая ценность волокон 1-2 ккал/г, но на практике ее полагают нулевой). Калорийность всех порций оказалась равной 243±5 ккал, что позволяет принять предположение без вопросов и доверять данным, за исключением одного продукта – кукурузных хлопьев с молоком, калорийность порции которых в 170 г оказалась равной 318 ккал.
Ошибка прозрачна – взято хлопьев на 240 ккал и 125 мл обезжиренного молока жирностью 1,5%, которые и дали избыточные 78 ккал. В других случаях, где к крупам добавлялось молоко, этого промаха сделано не было, количество круп было соответственно уменьшено, чтобы общая калорийность порции составляла 240 ккал. Нами кукурузные хлопья из рассмотрения исключены.
Также, после предварительного исследования, было принято решение исключить из рассмотрения вареный картофель, имеющий рекордно высокий ИС 323. Любой вариант подбора коэффициентов при факторах выводит оценку ИС за пределы 2 среднеквадратических отклонений экспериментального значения от среднего, что позволяет считать значение ИС картофеля выпадающим значением, выявление причин появления которого лежит за пределами нашего рассмотрения.
Учет этого продукта приведет к незначительном изменению подлежащих определению коэффициентов, и ухудшению погрешности оценки 36 оставшихся продуктов, не позволяя в любом случае хоть как-то улучшить подгонку под картофель.
Следующая задача – исключить факторы (компоненты), которые сильно связаны с другими факторами и порождают неустойчивость оценок коэффициентов. Анализ позволяет исключить фактор «сахара», после чего выявляется, что коэффициенты при крахмале и пищевых волокнах близки, и становится целесообразным сведение крахмала и волокон под одной переменной. Остаются 4 переменные – вес порции в г, количество белков, жиров, и суммарное количество крахмала с волокнами.
Устойчивое решение дает коэффициенты: 0,22; 1,72; 0,15 и 1,11, т.е. 1 г общего веса съеденного продукта или блюда дает 0,22 единицы сытости (ЕС), а 1 г белков, жиров или (крахмала + волокна) соответственно 1,72, 0,15 и 1,11 ЕС. По этим коэффициентам пересчитаны ИС всех 36 продуктов со сравнением с экспериментальными ИС. Сравнение отражено на диаграмме ниже, где вертикальные столбики – продукты с нижней и верхней границей ИС по экспериментальным данным, а точки – вычисленные по предлагаемой формуле значения. При этом следует иметь в виду, что границы вертикальных столбиков – это средние экспериментальные значения ±среднеквадратичные отклонения (сигма); следовательно, статистический разброс значений может быть еще шире.
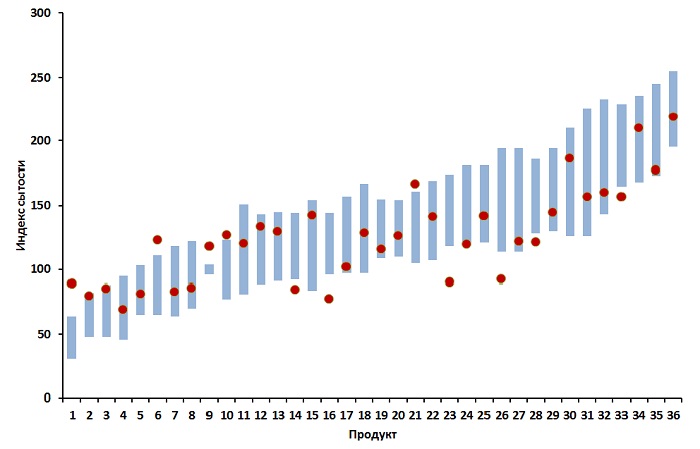
Продукты: 1 круассаны, 2 кекс, 3 пончики, 4 шоколадный батончик «Марс», 5 арахис, 6 йогурт (без сахара), 7 картофельные чипсы, 8 мороженое, 9 белый хлеб, 10 мюсли с молоком, 11 картошка фри, 12 пшеничные/рисовые поджаренные хлопья, 13 бананы, 14 мармелад «Желатиновые бобы», 15 макароны из муки тонкого помола, 16 печенье сладкое, 17 крекеры, 18 коричневый рис, 19 пшеница взорванная с медом, 20 фруктово-орехово-зерновая смесь, 21 чечевица, 22 белый рис (шлифованный), 23 сыр, 24 яйца, 25 пшеничные хлопья с молоком, 26 попкорн, 27 ржаной хлеб зерновой, 28 хлеб из непросеянной муки, 29 виноград, 30 вареные бобовые (фасоль, бобы), 31 говядина, 32 макароны из непросеянной муки, 33 яблоки, 34 апельсины, 35 овсяная молочная каша, 36 рыба (морская щука)
При нормальном распределении погрешностей в пределах ±1 сигма заключено 68% всех значений, здесь из 36 значений за границами оказываются 11 (5 выше и 6 ниже), т.е. формула с выведенными коэффициентами достаточно точно аппроксимирует экспериментальные данные.
Объединение под одной переменной крахмала и пищевых волокон удобно, поскольку эти компоненты структурно схожи, являются полимерами глюкозы, относятся к углеводам, и не всегда разделяются в таблицах состава продуктов. Разумеется, еще большее удобство бы предоставило включение в компонент (крахмал + волокна) других углеводов – сахаров, также включаемых в таблицах состава в углеводы, и подобная возможность была проверена, но, по причинам, по которым сахара были исключены уже на начальном этапе, включение в рассмотрение не оказывающих значимого влияние на ИС сахаров случайным образом смещает коэффициенты при факторах и ухудшает точность общей оценки.
Окончательная формула сытости любого количества продуктов следующая:
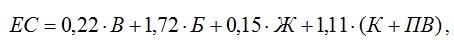
где ЕС – число единиц сытости; В – вес продукта в г, Б, Ж, К и ПВ – соответственно количество белков, жиров, крахмала и пищевых волокон в продукте или блюде. При подстановке значений В, Б, Ж, К и ПВ для размера порции в 240 ккал получаем значение индекса сытости ИС продукта.
Переходим к анализу выводов из формулы:
• белки действительно очень насыщают, их насыщающая способность самая высокая;
• вклад жиров в насыщаемость не отрицателен, но грамм жира насыщает в 10 раз меньше, чем грамм белков, с учетом более высокой калорийности жира разница еще более существенна;
• сахара исключаются из подсчета ИС, их вклад в сытость при смешанном питании нулевой;
• крахмал в составе хлеба, каш и пр. блюд – насыщает лучше, чем жир, притом при меньшей калорийности;
• пищевые волокна сами по себе никакой особой сытости продукту не придают, о косвенном их вкладе – ниже;
• основной источник насыщения – вес порции, определяемый в основном количеством содержащейся в блюде воды.
Пищевые волокна в желудке разбухают, образуя своеобразное желе, и сытость волокон определяется количеством выпитой воды. Отруби, содержащие большое количество волокон, добавляют для сытости к супам, жидким кашам и кисломолочным продуктам. Даже сухие отруби, попав в желудок, активно втягивают в себя воду из окружающих тканей, создавая субъективное чувство насыщения.
Подсчитаем из любопытства, сколько единиц сытости содержит средний рацион. За основу рациона можно взять формулу сбалансированного питания взрослого человека по А.А. Покровскому. По этой формуле суточная потребность взрослого человека составляет (взяты средние значения): белки 90 г, жиры 90 г, углеводы 450 г, из них сахар 75 г и крахмал 375 г, пищевые волокна (клетчатка и пектин) 25 г. Калорийность этого рациона 2970 ккал.
В формуле сбалансированного питания предусмотрено потребление общего количества воды (в среднем) 1975 мл, к чему следует прибавить вес компонентов 655 г, итого суммарный вес суточной пищи 2630 г. Подсчитаем суммарную сытость рациона в единицах сытости: 0,22 х 2630 + 1,72 х 90 + 0,15 х 90 + 1,11 х (375 + 25) = 1191 (ЕС). В среднем можно считать, что на каждую килокалорию равновесного рациона для создания сытости должно приходиться 0,4 ЕС.
А теперь посмотрим, что предлагается сделать для поднятия сытности низкокалорийного рациона. Большой популярностью пользуется система питания FAT30 с ограничением жиров до 30 г в день. Убрав 60 г жира, мы потеряем всего 9 ЕС, а недостающие 540 ккал восполним 135 дополнительными граммами белка, что составит 232 ЕС. Итого выигрыш 223 ЕС только за счет замены части жиров белками, что эквивалентно по сытости 500-600 ккал сбалансированного рациона. В результате такой замены компенсируется введенный для похудения дефицит калорий, за счет огромного ущерба для организма, связанного с нехваткой жиров и избытком белков.
Другой резерв увеличения суммарной сытности рациона – замена белками углеводов, впрочем, не такой эффективный, поскольку замена грамма углеводов граммом белка увеличит сытность всего на 0,6 ЕС. А вот употребление воды – поистине неограниченный источник сытности при нулевой калорийности воды и сытности 0,22 ЕС на каждый грамм. Общепринятой рекомендацией является употребление 8 стаканов или 2 литров чистой воды помимо жидкости, содержащейся в блюдах и напитках (по рекомендации диетолога М. Королевой «норма» поднята до 3 литров). 2 литра доставляют 440 ЕС, 3 литра – 660 ЕС. Тут речь идет уже о компенсации по сытности дисбаланса в 1000-1500 ккал, достаточно типичного для большинства низкокалорийных диет в 800-1200 ккал.
Отруби (пищевые волокна, клетчатка), рекомендуемые на диете Дюкана, и принимаются для связывания этого количества воды (доктор Дюкан также рекомендует пить не менее 2 л воды) и уменьшения чувства голода. При этом неизбежны риски вывода вместе с отрубями витаминов и минеральных веществ. Не зря ведь отруби категорически воспрещаются при приеме лекарств – лекарство не успеет усвоиться и начать действовать, как его попросят на выход.
Надеемся, что вы вместе с нами теперь разобрались в количественных соотношениях, увязывающих сытность пищи с ее компонентным составом и сопутствующим питьевым режимом.
Поскольку выводы основаны на результатах эксперимента, проведенного в камерных условиях, отвечающих режиму работы в офисе, их можно экстраполировать на режим работы с невысокой физической активностью и дробным питанием с интервалом между приемами пищи до 3 часов и нормальным питьевым режимом.
Выводы вряд ли удастся распространить на кето-диету или диету LCHF, где резко ограничивается количество углеводов при умеренном количестве белков и высоком количестве жиров, где мозг использует для питания не глюкозу, а кетоны, и все соотношения по сытости в маргинальных условиях выживания нарушаются.